Harry R. Schwartz

I’d heard a story that Stafford Beer—the pioneering British cyberneticist known for his work on the Viable System Model and the Cybersyn project¹ in Chile—once tried, in the 1960s, to turn the ecosystem of an English pond into a working computer.

Well, I thought, that sounds intriguing! So I set about hunting down the original source.

Andrew Pickering’s essay The Science of the Unknowable: Stafford Beer’s Cybernetic Informatics references a “brief report” by Beer from 1962 describing the experiment. That report, A Progress Note on Research Into the Cybernetic Analogue of Fabric, doesn’t seem to be on the Web, and as far as I can tell isn’t actually published anywhere any more, but I eventually found the text of it in a sketchy OCR’d EPUB file, cleaned it up, and reformatted it.

You can download the transcribed article as a PDF or read it directly below. I’ve inserted a few links to Wikipedia in the HTML version to help the reader.

I think this report is more interesting historically than scientifically. It’s a throwback to what I probably naively see as a sort of “romantic age” of computer science, when we weren’t yet quite sure what computing was, exactly, or how it would be implemented. And of course there’s still plenty of research being done on biological computing—even with crabs!—but it’s fun to imagine a world in which “environmental computing” became a dominant paradigm.

In particular, I love the inversion of thinking that this model suggests. As a programmer, I see a hive of bees and think about how I might model it in silico as a distributed system,² but what if instead I built a minimally complex computer system and outsourced the interesting distributed systems bits to an actual hive of bees? Imagine a world where AWS offered literal swarm computing, with a giant data center full of hives and criminally overworked beekeepers. What if I could implement an ant colony optimization using real ants? Or approximate a system of differential equations by sampling rabbit and fox populations?

These examples are whimsical and impractical, but Mechanical Turk operates on the same principles.

Dear sci-fi writers: please run with this. And please send me your manuscripts.

---

A Progress Note on Research Into a Cybernetic Analogue of Fabric

Stafford Beer
April 1962

In view of requests from several quarters for information about this problem, I compile the following notes. These are written for professionals in the field; that is, they assume familiarity with basic cybernetics. There is nothing at all definite to report: nothing, that is, that has been explored with sufficient thoroughness to warrant publication. Everything that follows is very much a spare time activity for me, although I am doing my best to keep the work alive—for I have a conviction that it will ultimately pay off. Ideally, an endowed project is required to finance my company’s Cybernetic Research Unit in this fundamental work.

The starting point for this thinking is to be found in chapter XVII of Cybernetics and Management (English Universities Press, 1959, John Wiley & Sons Ltd, 1960). It is argued there that a self-organizing system need not have its circuitry designed in detail—otherwise what virtue is there in the self-organizing capability? Furthermore, if systems of this kind are to be used for amplifying intelligence, or for “breeding” other systems more highly developed than they are themselves, a fixed circuitry is a liability. Instead, we seek a fabric that is inherently self-organizing, on which to superimpose (as a signal on a carrier wave) the particular cybernetic functions that we seek to model. Or, to take another image, we seek to constrain a high-variety fabric rather than to fabricate one by blueprint.

The Requirement

The basic mechanism for which we seek an appropriate fabric is undoubtedly that of the homeostat described by Ashby. This system offers a control mechanism that is ultrastable: a necessary feature of any control which is to deal with environmental disturbances of a kind not envisaged by the designer.

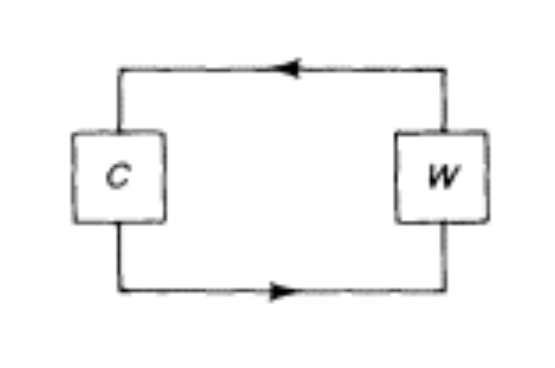
The essence of this control theory is that the outputs of a world situation are fed as inputs into a control mechanism, which in turn feeds its output into the world situation. This is to say that we set up a homeostatic relationship between the controller and the world (Figure 1). There seem to me to be just four basic requirements for a system of this kind.

1. That the variety of C ≥ the relevant variety of W
2. That the behaviour of each system can be transduced into the other (although not necessarily by linear transformation, nor indeed by any known transformation).
3. That the richness of interaction between C and W is high.
4. That the control system itself should be a homeostat

The reason for the first requirement is given by the law of requisite variety. The reason for the second is obvious, in that the systems must be coupled; the only point is whether much needs to be known about the actual parameters employed or the transformations involved. In view of the fact that each system is richly interactive internally, I cannot see that either matters very much: the overall system can be given the facility to learn how to weight its own output to achieve stable states more speedily if algedonic feedback provides a reward mechanism. The third point reflects the information-theoretic conditions governing channel capacity. The fourth requirement comes about because system C must be viable in its own right: it must keep its variety “on the boil,” ready to trap and deal with the disturbances reaching it.

Thus the problem with which we are first concerned is to construct system C, defined as a homeostat of high variety, which will simply go on operating—that is, will ceaselessly reach stable states and then disturb itself from them again. Such a system is in permanent oscillation, but is tending all the time towards stabilization.

A Review of Possible Fabrics

At the start of this work (in about 1954) I considered that electrical and electronic mechanisms should be discarded. They, it seemed, had to be designed in detail; and what kind of viable fabrics are glass and wire? However, in more recent years it has become clear that developments in solid-state physics may overcome this objection. For if it is possible to operate on the molecules of a germanium crystal, then we have a high-variety fabric which can be continuously constrained. Even so, the thinking that has been done about other kinds of fabrics should be recorded.

Chemical Systems

These are the machines I have labeled “fungoid.” My own experiments with them have not been very satisfactory: these have involved modifications of ideas developed by three other workers.

Firstly, there are Pask’s thread structures—depositions of metallic iron inside colloidal cells. Secondly, there is Chapman’s use of cotton threads soaked in sodium hydrochloride (which have the property of increasing their electrical resistance as they dry out with the repeated passage of electric current—and thereby model conditional probability learning devices).

Having collaborated with Pask in some of his work, I tried to simulate the undifferentiated networks of the reticular formation of the brain stem with his threads in three-dimensional spaces. I have not even met Chapman, but have tried to do the same with his cottons. Probably such a development as the latter requires close humidity control: at any rate, I got nowhere.

Thirdly, there is the attractive idea (suggested by George) that lipids might be used to create interfaces between cells. Semi-permeable membranes offer obvious advantages in any progress requiring selection and segregation. The need for them had been felt as the result of bifurcating Paskian colloidal cells with impermeable membranes. Fungoid machines, it was found, grew branches over plastic dividers—a gross sort of artefact of osmosis. But if (for example) lecithin sols could be used, they would form suitable membranes between any two aqueous liquids. The stability of such membranes, their viscosity, and their permeability to electrolytes, are dependent on many variables (such as temperature); in particular, the state of the cell itself (pH value) alters the characteristics of the membrane. Thus thresholds could in principle be modified by feedback from the amount of intracellular activity—a conditional probability learning trick.

The biological controls needed to handle lecithin aseptically were beyond the capability of my laboratory, and collaborators thought that it would be unnecessary to use organic material at all. Even so, it is worth recording the idea: simplicity and smallness are important in this kind of engineering (because of the enormous numbers of components involved), and interfaces that are themselves both structural components and system variables are appealing.

Human Beings

In 1956 I devised a game for solving simultaneous linear equations in two variables. The theory used the properties of groups to simplify the arithmetic: the game worked in homomorphic transformations modulo 5. It was played by unsophisticated persons, such as children, who could not be expected to know everything about simultaneous equations. They competed with each other to make correct selections from sets of five, and then to synthesize the selections and select therefrom, by means of a simple machine. This simulated algedonic feedback by means of coloured lights which announced that “pleasure” or “pain” was being experienced.

The idea of this was to demonstrate the possibility of intelligence amplification. Intelligence, in the sense of an ability to steer one’s way from pain to pleasure within a simple game language, was certainly amplified in that (unknown to the competitors) the equations were actually solved. Was any particular solution implicit in the game language? I think not; because the game could and did handle actual equations which had not been previously studied by the inventor. This series of experiments was entirely successful; unfortunately the opportunity to write them up for publication has now been lost.

The extension of this work was intended to be as follows. By using human beings, one reduces the technical problems of communication—the experimenter and the system could talk to each other. But in so far as all this worked, it seemed in principle possible to use any other kind of animal for the purpose. Some effort was made to devise a “mouse” language which would enable mice to play this game—with cheese as a reward function. The advantages of using animals are clear: in addition to any language imposed upon them by the scientist, they presumably have their own mouse language. That is, they live in communities and communicate. Such a community obviously constitutes a high-variety self-organizing fabric from the “systems” point of view.

Vertebrates

In this way I was led to consider various kinds of animal, and various sorts of language (by which I mean intercommunicating boxes, ladders, see-saws, cages connected by pulleys and so forth). Rats and pigeons have both been closely studied for their learning attributes, both as individuals and as groups, by many workers; they seemed possible components for a system. The Machina Speculatrix of Grey Walter might also be considered (with apologies to the organic molecule) as a vertebrate for such purposes. Consider, for example, an animated nomograph. This would be driven by two animals, intercommunicating in the sense that each is aware of the activities of the other at the opposite end of the cursor. A coupled arrangement of two such nomographs was designed to play the simultaneous equations game. However, no actual machines were built.

Social Insects

By the same token, bees, ants, termites, have all been systematically considered as components of self-organizing systems, and various “brainstorming” machines have been designed by both Pask and myself. But again none has been made.

Animalcules

One of Pask’s designs used Aedes Aegypti, the larva of the yellow fever mosquito; and I designed another incorporating Daphnia, the freshwater crustacean.

Many experiments were made with the latter machine. Iron filings were included with dead leaves in the tank of Daphnia, which ingested sufficient of the former to respond to a magnetic field. Attempts were made to feed inputs to the colony of Daphnia by transducing environmental variables into electromagnets, while the outputs were the consequential changes in the electrical characteristics of the phase space produced by the adaptive behaviour of the colony.

Be it noted that a system of this kind retains stochastic freedom within the pattern generally imposed—a necessary condition in this kind of evolving machine; it is also self-perpetuating, and self-repairing, as a good fabric should be. However, there were many experimental problems. The most serious of these was the collapse of any incipient organization—apparently due to the steadily increasing suspension of tiny permanent magnets in the water.

“Gas Particles”

Next were considered the very small organisms which because of their great numbers can be regarded as a “biological gas,” and are interactive but independent entities. Amoebae and others have been considered. The protozoon Euglena seemed to have special attractions.

This is a photosynthetic free-swimming protozoon, which in culture offers an unconstrained fabric of high variety, having the capacity to respond (in a well-documented way) to a variety of stimuli with detectable behaviour. When we started this work, we thought Euglena was relatively easy to culture in an inorganic solution (plus traces of organic factors).

Euglena is sensitive to light: the tropism reverses after illumination has reached a critical value. It is also sensitive to heat, chemicals and mechanical shock. As its metabolism depends on light, the normal positive response to light would be reinforced by reproduction (binary fission—reproduction by fusion unknown). In the prolonged absence of light, the beast loses its chlorophyll and tries to make a living on the organic matter in the medium.

As to interaction, several Euglena in a culture will affect each other in a number of ways:

1. By reducing the nutrient concentration of the medium
2. By blocking light paths, which will interfere with the phototropic and photosynthetic activities of those to leeward.
3. By their waste products

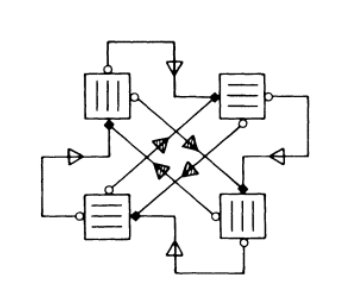
The design shown in Figure 2 was made for this system. It is evident from this design that the two sensory receptors are logical contraries. In fact, there is of course no need for more than one actual cell, which would relay a stimulating impulse to one of its target cultures and an inhibiting impulse to the other.

It seems that this system should tend to an equilibrial state, but that chance variables are likely to procure step functions in the system, thereby meeting the “on the boil” criterion.

It was found possible to read in and out of the cultures, using a point source of light as the stimulus, and a photocell as the sensory receptor. However, the culturing difficulties proved enormous. Euglena showed a distressing tendency to lie doggo, and attempts to isolate a more motile strain failed.

Working with Euglena brought home the factors already mentioned as relative to this problem. Each small tank of greenish liquid contained several million independent creatures behaving in complex ways, photosynthesizing and reproducing interminably: a staggering source of high variety. The reinforcement given by the loop “more light → more photosynthesis → more Euglena → more light” could be viewed as an algedonic control: it is essentially a reward mechanism.

Ponds

So pure cultures were difficult to handle. Moreover, they are not, perhaps, ecologically stable systems. Dr Gilbert, who had been trying to improve the Euglena cultures, suggested a potent thought. Why not use an entire ecological system, such as a pond? The theory on which all this thinking is based does not require a knowledge of the black box employed.

Accordingly, over the past year, I have been conducting experiments with a large tank or pond. The contents of the tank were randomly sampled from ponds in Derbyshire and Surrey. Currently there are a few of the usual creatures visible to the naked eye (Hydra, Cyclops, Daphnia, and a leech); microscopically there is the expected multitude of micro-organisms. In this tank are suspended four lights, the intensities of which can be varied to fine limits. At other points are suspended photocells with amplifying circuits which give them very high sensitivity. Roughly, I am trying to treat this system in the way designed for Euglena, superimposing the four tanks of Figure 2 on to each other in the one tank. There is an ecological guarantee that this system stabilizes itself, and is indeed ultra-stable. But, of course, the problem of making it act as a control system is very difficult indeed.

I regard the machine as a tending-to-be-stable-but-not-quite homeostat, like the box labeled C in Figure 1. Events in the world (W) have to be transduced into the control machine, thus providing an independent modification of the light sources. The stochastic variety of the control machine must then absorb the world variety and demonstrate the phenomena we are anxious to display. But the channel capacity of the photoelectric feedback to the world situation is insufficient to resolve the ambiguity of the signals in the tank. In other words, at present there seems no way of meeting the requirements of Shannon’s Tenth Theorem. Also, there ought to be some way of nominating a threshold below which the rate of change in the homeostat of this not-quite-stable system would be deemed to represent stability. I do not know how to measure this.

The state of this research at the moment is that I tinker with this tank from time to time in the middle of the night. My main obsession at the moment is at the level of the philosophy of science. All this thinking is, perhaps, some kind of breakthrough; but what about an equivalent breakthrough in experimental method? Do we really know how to experiment with black boxes of abnormally high varieties?

Our scientific training, modified as it may be by years of experience in cybernetics, pushes us always towards attempts at analysis. I tell myself repeatedly that this thing is a black box in whose transfer functions I am not interested. Yet I repeatedly try to isolate experimental effects: to discover light intensities at which attraction flip-flops to repulsion for the creatures operating in the zone between a light and a photoreceptor, for instance. I do not want to do this, but I do it. The reason is, of course, that although one can see experimental techniques for handling the total system and measuring its behaviour, the results defy the kinds of interpretation at our disposal.

Perhaps the next step is to think of a small, readily examined, uncontrolled system to represent “the world.” It might then be possible to couple it to the tank and measure the extent of control. Has anyone any ideas? At the least, a reader unconventional enough in his scientific outlook to have read these notes to this point selects himself as having a sufficiently bizarre mind to help!